la fisica del presente respaldada por la del pasado

sábado, 4 de septiembre de 2010

MOVIMIENTO ARMÓNICO SIMPLE ( M.A.S )

El movimiento armónico simple (se abrevia m.a.s.) es un movimiento periódico que queda descrito en función del tiempo por una función armónica (seno o coseno). Si la descripción de un movimiento requiriese más de una función armónica, en general sería un movimiento armónico, pero no un m.a.s..

En el caso de que la trayectoria sea rectilínea, la partícula que realiza un m.a.s. oscila alejándose y acercándose de un punto, situado en el centro de su trayectoria, de tal manera que suposición en función del tiempo con respecto a ese punto es unasinusoide. En este movimiento, la fuerza que actúa sobre la partícula es proporcional a su desplazamiento respecto a dicho punto y dirigida hacia éste.

OSCILACIÓN :

es un viaje de ida y de vuelta
la máxima distancia que recorre el péndulo desde el punto de equilibrio se llama amplitud

En un movimiento Armónico simple hay dos amplitudes
la distancia que hay desde el punto de equilibrio a una posición antes de la amplitud se llama elongación

elongación : amplitud

PERIODO: es el tiempo que demora en realizar una oscilación completa ( ida y vuelta )

EJEMPLOS :

PÉNDULO:
RESORTE :

Ecuación del movimiento


Elongación

En un movimiento armónico simple la magnitud de la fuerza ejercida sobre la partícula es directamente proporcional a su elongación, esto es la distancia x\, a la que se encuentra ésta respecto a su posición de equilibrio. En un desplazamiento a lo largo del eje Ox, tomando el origen O en la posición de equilibrio, esta fuerza es tal que F_{x} = - kx\, donde k\, es una constante positiva y x\, es la elongación. El signo negativo indica que en todo momento la fuerza que actúa sobre la partícula está dirigida hacía la posición de equilibrio; esto es, en sentido contrario a su elongación (la "atrae" hacia la posición de equilibrio).

Aplicando la segunda ley de Newton, el movimiento armónico simple se define entonces en una dimensión mediante la ecuación diferencial

(1) m \frac{d^{2}x}{dt^{2}} = -k x

Siendo m\, la masa del cuerpo en desplazamiento. Escribiendo 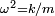\scriptstyle \omega^{2} = k/m se obtiene la siguiente ecuación donde ω es la frecuencia angulardel movimiento:

(2) \frac{d^2x}{dt^2} = a(t) = -\omega^2x

La solución de la ecuación diferencial (2) puede escribirse en la forma

(3) x(t) = A \cos(\omega t + \phi)\,

donde:

x\, es la elongación de la partícula.
A\, es la amplitud del movimiento (elongación máxima).
\omega\, es la frecuencia angular
t\, es el tiempo.
\phi\, es la fase inicial e indica el estado de oscilación o vibración (o fase) en el instante t = 0 de la partícula que oscila.

Además, la frecuencia de oscilación puede escribirse como

(4)f = \frac{\omega}{2 \pi} = \frac{1}{2 \pi} \sqrt{\frac{k}{m}}, y por lo tanto el periodo como T = \frac{1}{f} = \frac{2 \pi}{\omega} = 2 \pi \sqrt{\frac{m}{k}}

La velocidad y aceleración de la partícula pueden obtenerse derivando respecto del tiempo la expresión x(t) = A \cos(\omega t + \phi)\,.


[editar]Velocidad

La velocidad se obtiene derivando la ecuación de la posición obtenida en el apartado anterior respecto al tiempo:


(5) x = - \omega A \, \sin(\omega t + \phi)


Aceleración

La aceleración es la variación de la velocidad del movimiento respecto al tiempo y se obtiene por lo tanto derivando la ecuación de la velocidad respecto al tiempo:

(6) a(t) = \frac{dv(t)}{dt} = -\omega^2 A \, \cos(\omega t + \phi) = -\omega^2 x(t)\,


Amplitud y fase inicial

La amplitud A y la fase inicial \phi\, se pueden calcular a partir de las condiciones iniciales del movimento, esto es de los valores de la elongación x0 y de la velocidad v0 iniciales.

(7) x_{0} = A \cos\phi \qquad\Rightarrow\qquad x_{0}^2 = A^{2} \cos^{2} \phi

(8) v_{0} = - \omega A \sin \phi \qquad\Rightarrow\qquad v_{0}^{2} = \omega^{2} A^{2} \sin^{2} \phi \qquad\Rightarrow\qquad \frac{v_{0}^{2}}{\omega^{2}} = A^{2} \sin^{2} \phi

Sumando miembro a miembro las dos ecuaciones (4a) y (4b) obtenemos

(9) x_{0}^{2} + \frac{v_{0}^{2}}{\omega^{2}} = A^{2} (\cos^{2} \phi + \sin^{2} \phi) = A^{2} \qquad\Rightarrow\qquad A = \sqrt{x_{0}^{2} + \frac{v_{0}^{2}}{\omega^{2}}}

Dividiendo miembro a miembro las dos ecuaciones (4b) y (4a) obtenemos

(10) \frac{v_0}{x_0}= \frac{-\omega A\sin\phi}{A\cos\phi}=-\omega\tan\phi \qquad \Rightarrow \qquad \phi =\arctan\left(-\frac{v_0}{\omega x_0}\right)

Publicado por en

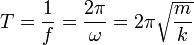
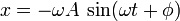
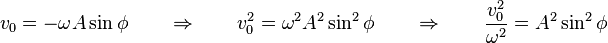
No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)